This is so easy, someone else should have done it already. There is some code here: http://www.mathworks.co.uk/matlabcentral/fileexchange/25528-line-clipping. However, among other things (like using input), it doesn't check for lines parallel with the clipping window borders.

Wikipedia gives a variety of algorithms -- Liang/Barsky's algorithm is probably the one which one implement most quickly.

Here goes the code:

function [xx1, xx2] = clipped_line(vx1, vx2, v1, v2)
% function [xx1, xx2] = clipped_line(vx1, vx2, v1, v2)
% 
% Liang-Barsky Algorithm for line clipping. See
% http://en.wikipedia.org/wiki/Liang%E2%80%93Barsky_algorithm
%
% Take a 2-D line from vx1 to vx2, and clip to rectangle with corners at
% v1, v2.
% 
% Inputs must be vectors of length 2.
% Outputs are vectors of length 2. If no outputs are specified, a plot is
% made.
%

    if length(vx1) ~= 2 || length(vx2) ~= 2 || length(v1) ~= 2 || length(v2) ~= 2
        error('All inputs must be vectors of length 2.');
    end

    x0 = vx1(1);
    x1 = vx2(1);
    y0 = vx1(2);
    y1 = vx2(2);
    
    x_min = min(v1(1), v2(1));
    x_max = max(v1(1), v2(1));
    y_min = min(v1(2), v2(2));
    y_max = max(v1(2), v2(2));

    xx1 = nan(size(vx1));
    xx2 = nan(size(vx2));
    
    dx = x1 - x0;
    dy = y1 - y0;
    
    p = [ -dx; 
           dx; 
          -dy;
           dy ];

    q = [ x0 - x_min;   % negative => left of window 
          x_max - x0;   % negative => right of window 
          y0 - y_min;   % negative => below window
          y_max - y0;   % negative => above window
        ];
              
% Test if line isn't visible.
%     for i = 1:4
%         if p(i) == 0 && q(i) < 0
%             return;
%         end
%     end
    if ~isempty(find(p == 0 & q < 0, 1, 'first'))
        return;
    end
    
    u1 = 0;
    u2 = 1;
    
    for i = 1:4
        if p(i) < 0
            u1 = max(u1, q(i)/p(i));
        end
        if p(i) > 0
            u2 = min(u2, q(i)/p(i));
        end
    end
    
    if u1 > u2  % line is outside
        return;
    end
    
    xx1(1) = x0 + dx*u1;
    xx1(2) = y0 + dy*u1;

    xx2(1) = x0 + dx*u2;
    xx2(2) = y0 + dy*u2;

    if nargout == 0
        rectangle('position', [x_min y_min (x_max-x_min) (y_max-y_min)]);
        
        l1 = line([x0 x1], [y0 y1]);
        set(l1, 'color', 'k', 'linestyle', '--');
        hold all
        l2 = plot([xx1(1) xx2(1)], [xx1(2) xx2(2)], 'o-');
        set(l2, 'linestyle', '-', 'linewidth', 2);
        
        xlim([ min([x0, x1, x_min])-.1, max([x0, x1, x_max])+.1 ]);
        ylim([ min([y0, y1, y_min])-.1, max([y0, y1, y_max])+.1 ]);
    end
    
end

Now, running this:

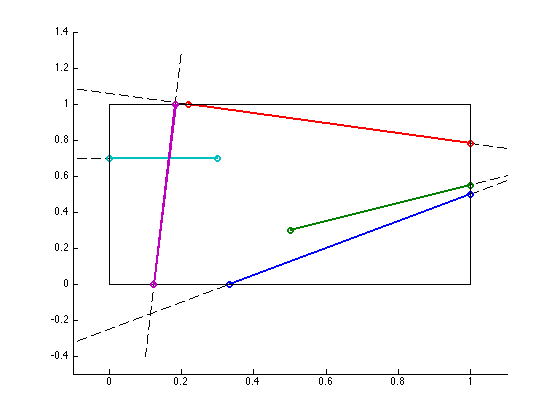
figure; 

clipped_line([-1, -1], [3, 2], [0 0], [1 1]); 
clipped_line([0.5, 0.3], [1.3, 0.7], [0 0], [1 1]);
clipped_line([-0.5, 1.2], [1.3, 0.7], [0 0], [1 1]);
clipped_line([-0.5, 0.7], [0.3, 0.7], [0 0], [1 1]);
clipped_line([0.2, 1.3], [0.1, -0.4], [0 0], [1 1]);

Makes this: